Bài toán này xuất phát từ một trò chơi truyền hình nổi tiếng của Mỹ là Let’s make a deal với người dẫn chương trình đồng thời cũng là đồng sáng lập trò chơi tên là Monty Hall.

Giả sử bạn là thí sinh tham dự chương trình. Bạn bước vào một vòng thi, trước mặt bạn là 3 cánh cửa đánh số 1,2,3. Monty cho bạn biết bên trong 3 cửa này có 2 cửa là con dê, cửa còn lại là chiếc xe hơi Venedo Roadster của hãng Lamborghini có giá trị đến 4.5 triệu USD.
Bạn được quyền chọn 1 trong 3 cánh cửa này, nếu sau cánh cửa đó là xe hơi thì bạn sẽ được thưởng xe hơi. Nhưng nếu sau cánh cửa đó là con dê, bạn phải mang nó về. Vậy câu hỏi được đặt ra là làm thế nào để chọn được cửa có xe hơi, hay chọn cửa có xác suất trúng xe hơi cao nhất? Hiện ta chưa có dữ kiện nào để dự đoán nên nếu ta chọn ngẫu nhiên 1 cửa bất kỳ, do trong 3 cửa này chỉ có một cửa có xe hơi nên xác suất để ta trúng được xe hơi là 1/3 và xác suất trúng con dê là 2/3. Ta sẽ chọn ngẫu nhiên một cửa, cửa số 1 chẳng hạn.
Monty Hall đương nhiên biết cửa nào có xe hơi, cửa nào có dê. Sau khi bạn chọn cửa số 1, Monty sẽ mở cửa số 2, bên trong đó là con dê xuất hiện.
Sau đó, Monty sẽ hỏi bạn rằng bạn muốn giữ lại cửa số 1 hay thay đổi quyết định sang cửa số 3. Theo bạn, bạn sẽ làm gì? Có lẽ nhiều bạn xem bài viết này sẽ nhận định rằng giữ lại hay thay đổi thì…cũng vậy, ta vẫn không biết cửa nào có xe, cửa nào có dê nên xác suất ta trúng xe là 50:50 hay 1/2 nên việc giữ hay đổi đều mang tính may rủi là chính. Nghe có vẻ hợp lý chứ nhỉ?
Để đơn giản hóa vấn đề, ta hãy thiết lập hết tất cả các trường hợp xảy ra. Cụ thể như sau:
Ta có các cách sắp xếp 1 chiếc xe hơi, 2 con dê vào 3 cửa được đánh số theo thứ tự 1,2,3 với các trường hợp như sau (X là xe hơi, D là con dê):
– Xét trường hợp X,D,D Bạn chọn cửa 1, Monty sẽ mở cửa 2 hoặc 3. Nếu bạn đổi, bạn được dê, nếu bạn không đổi, bạn được xe.
– Xét trường hợp D,X,D: Bạn chọn cửa 1, Monty sẽ mở cửa 3. Nếu bạn đổi, bạn được xe, nếu bạn không đổi, bạn được dê.
– Xét trường hợp D,D,X: Bạn chọn cửa 1, Monty sẽ mở cửa 2. Nếu bạn đổi, bạn được xe, nếu bạn không đổi, bạn được dê.
Qua 3 trường hợp, bạn thấy rằng nếu như bạn không đổi, xác suất bạn được xe là 1/3, còn nếu bạn đổi thì xác suất đã tăng lên đến 2/3. Vậy cách tốt nhất đó là bạn hãy đổi cửa sẽ cho bạn khả năng trúng được xe cao nhất.
Bạn ngạc nhiên lắm đúng không? Hãy mở rộng bài toán, thay vì lúc đầu bạn chọn cửa số 1 thì bây giờ bạn chọn ngẫu nhiên 1 trong 3 cửa. Vẫn làm theo cách thủ công như trên với trường hợp bạn chọn cửa số 2, số 3, bạn vẫn ra xác suất trúng xe hơi khi giữ cửa là 1/3 và khi đổi cửa là 2/3.
Có vẻ bạn vẫn có gì đó vướng mắc trong lòng đúng không? Vậy ta tiếp tục mở rộng bài toán thành 100 cửa, trong đó 99 cửa có con dê và chỉ duy nhất 1 cửa có xe hơi. Cũng với cách chơi đó, bạn nghĩ cửa nào sẽ có xe hơi? Thật khó để đoán chính xác đúng không vì xác suất bạn chọn trúng cửa có xe hơi là 1% trong khi 99% bạn sẽ chọn trúng cửa có dê.
Giả sử bạn chọn cửa số 1, đương nhiên bạn sẽ không mấy an tâm về chiếc xe hơi có sau cánh cửa này (trừ khi bạn biết trước kết quả). Có thể bạn nghĩ chiếc xe nằm ở cửa 69 hay 35 hay 100, …
Tiếp theo, Monty mở 98 cửa, trừ cửa bạn chọn và cửa 37. Monty hỏi bạn giữ hay đổi? Lúc này, nếu bạn đổi thì xác suất bạn trúng được chiếc xe là 99% đấy, và bản thân bạn cũng dự đoán trong lòng là cửa có xe phải nằm ở con số nào “lớn lớn tí” đúng không?
Ta thấy rằng xác suất chọn cửa có xe hơi đã thay đổi khi Monty mở cửa có dê. Hay nói cách khác, xác suất của một biến cố thay đổi khi ta có thêm thông tin liên quan đến biến cố đó. Đây là một vấn đề toán học cơ bản đã được Rev Thomas Bayes – nhà thống kê người Anh, nghiên cứu và phát triển vào giữa thế kỷ XVIII
Bayes đã phát triển 1 định lý mà ngày nay được mang tên ông. Định lý Bayes sẽ giúp chúng ta trả lời câu hỏi nên giữ cửa hay đổi bằng toán học. Định lý này nói về khả năng tương quan giữa 2 sự kiện xảy ra đồng thời.
Hai sự kiện trong bài toán Monty Hall trên đó là xác suất để chiếc xe hơi nằm sau cửa số 1 (cửa ban đầu bạn chọn) và xác suất để Monty mở cửa số 2 (điều mà ông ta đã làm). Đặt X là sự kiện chiếc xe hơi nằm sau cửa số 1, Y là sự kiện Monty mở cửa số 2. Rev Thomas Bayes cho ta công thức tính 2 sự kiện xảy ra cùng nhau X và Y là:
P(X∩Y)=P(X|Y)P(Y)
với P(X|Y) là xác suất của biến cố X khi biến cố Y xảy ra, cụ thể trong bài toán trên đó là nếu như Monty mở cửa số 2 thì xác suất chiếc xe nằm ở cửa số 1 là bao nhiêu? P(Y) là xác suất xảy ra biến cố Y, tức xác suất mà Monty mở cửa số 2. Đây chính là công thức xác suất có điều kiện, gọi là công thức Bayes.
Mặt khác P(X∩Y)=P(Y∩X) nên ta có thể viết công thức Bayes thành:
P(Y∩X)=P(Y|X)P(X)
Từ đó ta có công thức:
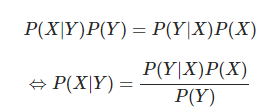
Phân tích một chút về phương trình này, P(Y|X) có nghĩa là xác suất để Monty mở cửa số 2 khi chiếc xe hơi nằm ở cửa số 1, xác suất này nghĩa là gì? Giả sử chiếc xe ở cửa số 1 thì xác suất để Monty mở cửa số 2 là 1/2 hay 50% vì Monty chỉ có thể mở cửa số 2 hoặc 3 và ông ta thừa biết sau 2 cửa đó là con dê. Vậy P(Y|X)=1/2.
Chưa hết, ta cần tính xác suất chiếc xe ở cửa số 1, tức tính P(X) Trên thực tế, người chơi hoàn toàn không biết chiếc xe hơi ở đâu trong 3 cửa này nên ta được P(X)=1/3. Còn xác suất để Monty mở cửa số 2 là P(Y)=1/2. Vậy, ta được:
P(X|Y)=P(Y|X)P(X)P(Y)= 1/2*1/3/1/2=1/3
Vậy khi Monty mở cửa số 2, xác suất để chiếc xe ở cửa số 1 là 1/3. Mặt khác, trong hai cửa 1 và 3 chắc chắn có một cửa có xe hơi nên giả sử ta đặt Z là biến cố xe nằm ở cửa số 3, dễ thấy 2 biến cố X và Z xung khắc nhau do xe chỉ nằm ở 1 trong hai cửa chứ không thể nằm ở cả hai nên ta có phương trình:
P(X)+P(Z)=1
⇔P(Z)=1−P(X)=1−1/3
⇔P(Z)=2/3
Như vậy xác suất để xe nằm ở cửa số 3 là 2/3 hay 66,67%. Vì vậy khi Monty hỏi bạn có đổi sang cửa số 3 hay giữ lại cửa số 1 thì tốt nhất bạn nên đổi sang cửa số 3 vì điều này sẽ làm cho xác suất bạn trúng xe hơi cao hơn.
Điều này có đảm bảo chắc chắn bạn sẽ trúng xe hơi không? Rất tiếc là không, nó chỉ làm tăng khả năng bạn thắng xe hơi mà thôi. Nhưng nếu như bạn chơi nhiều lần thì xét về mặt trung bình, chiến thuật đổi cửa này sẽ giúp bạn có được xe hơi trong 2/3 lần bạn chơi đấy.
Lịch sử của bài toán này rất thú vị, nó được công bố lần đầu tiên bởi Steve Selvin (Giáo sư thống kê sinh học, trường Đại học California, Berkeley) trên Tạp chí thống kê Mỹ vào năm 1975. Ngay sau đó có đến hàng chục ngàn bức thư phản hồi cho rằng việc đổi cửa làm tăng khả năng chiến thắng là sai, dù bạn có đổi hay không thì xác suất bạn trúng xe hơi là 50:50 hay 1/2. Điều đặc biệt là trong số hàng chục ngàn bức thư ấy có khoảng một ngàn bức thư được viết bởi những người làm toán chuyên nghiệp trình độ Tiến sĩ, trong đó có cả Paul Erdõs, ông ta rất hoài nghi và chỉ chấp nhận kết quả khi tận mắt chứng kiến kết quả mô phỏng bài toán Monty Hall trên máy tính.
Trên thực tế bài toán này đã xảy ra ở trò chơi Deal or no deal tại Mỹ (tạm dịch: Đi tìm ẩn số). Ở vòng chơi cuối cùng sẽ có 26 cặp với 26 mệnh giá khác nhau, thấp nhất là 0.5 USD và cao nhất là 1.000.000 USD, người chơi sẽ giữ 1 cặp và mở các cặp còn lại. Ta có thể so sánh giá trị tương quan rằng cặp mang giá trị 1.000.000 USD ứng với cửa có chiếc xe hơi, các cặp còn lại ứng với cửa có dê.
Lúc đầu, người chơi tên là Richie Bell giữ cặp số 15. Ở lượt cuối cùng chỉ còn 2 cặp là cặp 15 cặp mà Richie đang giữ) và cặp 1 ở trên sân khấu, một cặp là 1 USD (≈23.500 VNĐ, ứng với con dê) và một cặp là 1.000.000 USD (≈2.350.000.000VNĐ, ứng với chiếc xe). MC của chương trình là Howie Madel đã hỏi Richie có muốn đổi sang cặp 11 hay không? Dễ tính được nếu Richie giữ cặp thì xác suất anh ta thắng giải triệu đô là 1/26, trong khi nếu anh ta đổi thì xác suất sẽ tăng lên 25/26. Tiếc là Richie đã không đổi và kết quả khi mở cặp 15 của anh ta là 1 USD.
Tuy nhiên, xác suất để chiến thắng giải triệu đô khi giữ cặp dù nhỏ nhưng vẫn có thể xảy ra. Tại trò chơi Đi tìm ẩn số tại Anh, có 2 chiếc hộp đỏ với mệnh giá thấp nhất là 1p đến 250.000 bảng Anh. Vào ngày 12/2/2014, người chơi tên Roop Sings chọn hộp số 2. Sau một số lần chơi, trên sân khấu chỉ còn hộp số 2, một trong hai hộp này sẽ có giá 250.000 bảng Anh, hộp còn lại là 500 bảng Anh. Người dẫn chương trình hỏi Roop có muổn đổi hộp không và ông ta quyết định không đổi. Kết quả, Roop Sings nhận được giải thưởng 250.000 bảng Anh.