Một số trò chơi thường thiên về may mắn, như khả năng chiến thắng của bạn dựa trên xúc xắc bạn lắc hay lá bài bạn được phát. Nhưng vẫn có những trò chơi cần chiến lược, nếu bạn chơi khéo léo, bảo đảm bạn sẽ giành chiến thắng.
Một ví dụ đó là trò chơi Nim, một trò chơi cổ xưa. Cho dù trò chơi đang ở giai đoạn nào, ta luôn có một chiến thuật thắng cho một trong hai người chơi, và một hình thức bổ sung rất thú vị sẽ cho bạn biết ai là người chiến thắng.
I. LUẬT CHƠI NIM
Trò chơi truyền thống Nim được chơi với một số đồng xu được sắp xếp thành nhiều đống, cách sắp số lượng đồng xu và đống tùy thuộc vào bạn. Có hai người chơi, khi đến lượt, người chơi có thể lấy một số lượng tùy ý đồng xu từ một đống duy nhất. Họ phải lấy ít nhất 1 đồng xu và họ không được lấy các đồng xu từ đống khác. Người thắng là người lấy đồng xu cuối cùng, nghĩa là không còn đồng xu nào sau nước đi của người đó. (Một số người chơi có cách chơi khác, người lấy đồng xu cuối cùng sẽ thua, nhưng hiện tại chúng ta sẽ bỏ qua phiên bản đó)
Rõ ràng ở đây không có sự may mắn. Bạn có thể tìm ra nước đi tốt nhất bằng việc dự đoán kết quả của nước đi trước đó một cách khéo léo.
Ví dụ về cách chơi trò này như sau: Giả sử có 3 đống, mỗi đống lần lượt có 3,4,5 đồng xu. Sau đây là quy trình chơi:
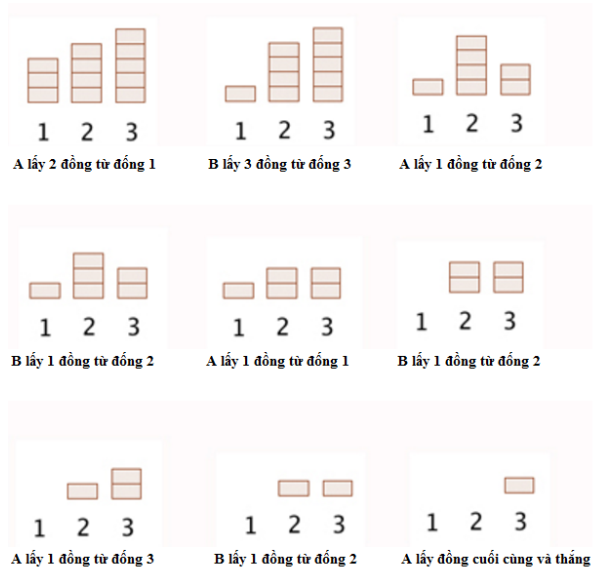
Trò chơi Nim bắt đầu với 3 đống với mỗi đống lần lượt có 3,4,5 đồng xu. A là người chiến thắng
Câu hỏi mà chúng ta quan tâm là: Cho một trạng thái cụ thể các đống và đồng xu, liệu có một chiến lược thắng cho một trong các người chơi? Nghĩa là, liệu có một người chơi được đảm bảo sẽ thắng nếu người đó đi đúng bước?
Hãy bắt đầu với một vài ví dụ. Giả sử có 2 người chơi A và B, A là người đi trước. Giả sử có 2 đống, mỗi đống có 1 đồng xu. Rõ ràng, B là người chiến thắng vì A buộc phải lấy 1 trong 2 đồng xu, để lại cho B lấy đồng cuối cùng.
Bây giờ giả sử có 2 đống, một đống có 2 đồng xu, đống còn lại có 1 đồng xu. Người chơi A sẽ có chiến lược thắng: Lấy 1 đồng từ đống có 2 đồng xu. Khi đó ta còn lại 2 đống, mỗi đống 1 đồng xu và người chơi B đi tiếp. Như ví dụ trước, A là người thắng cuộc.
Chúng ta cùng làm thêm một ví dụ nữa: Giả sử có 2 đống với 2 đồng xu mỗi đống. Lúc này B sẽ là người có chiến thuật thắng. Nếu A lấy hết một đống, B chỉ cần lấy đống còn lại và thắng. Nếu A chỉ lấy 1 đồng của một đống thì chúng ta trở về lại trường hợp trên với B đi trước. Do đó B luôn đảm bảo sẽ thắng nếu B lấy 1 đồng từ đống có 2 đồng xu.

Ai có chiến lược thắng?
Từ chuỗi ví dụ trên, bạn có thể cảm giác rằng có một mô hình nào đó cho trò chơi này: Cho một cách sắp xếp các đống và các đồng xu, sẽ có một chiến lược thắng cho một trong hai người chơi. Nhà toán học Charles Bouton (1869-1922) cũng cảm thấy điều tương tự và đặt mình vào nhiệm vụ khó khăn là phân tích toàn bộ trỏ chơi trên. Năm 1902 ông đã tìm ra bí quyết – và bí quyết này thật tinh tế! Để tìm ra có một chiến thuật thắng cho người chơi, đầu tiên bạn cần phải …
II. SỬ DỤNG DÃY NHỊ PHÂN
Bí mật ở đây chính là viết số lượng đồng xu trong các đống thành số nhị phân. Để biết làm như thế nào, cần nhớ lại cách viết số thập phân thông thường như thế nào. Lấy 4302 làm ví dụ, 4 ở đây không đơn thuần chỉ là số 4, mà lã 4000 hay 4×10004×1000. Tương tự, 3 không đơn thuần chỉ là số 3 mà là 300=3×100300=3×100, 0 đại diện cho 0×100×10, và 2 đại diện cho 2×12×1. Như vậy 4302 nghĩa là:
4×1000+3×100+0×10+2×14×1000+3×100+0×10+2×1
Tương tự số 7396 được biểu diễn là
7×1000+3×100+9×10+6×17×1000+3×100+9×10+6×1
Các số 1000, 100, 10 và 1, xuất hiện ở các biểu thức trên có điểm chung là gì? Chúng đều là lũy thừa của 10
1000=1031000=103
100=102100=102
10=10110=101
1=1001=100
Để viết các số theo hệ thập phân, đầu tiên bạn cần phải viết chúng dưới dạng tổng liên tiếp các lũy thừa của 10 (với lũy thừa lớn nhất ở bên trái), và sau đó viết các hệ số của các lũy thừa đó. Chúng ta có thể làm tương tự với lũy thừa của 2 thay vì 10. Ví dụ, giá trị của dãy nhị phân 110 viết dưới hệ thập phân là:
1×22+1×21+0×20=4+2+0=61×22+1×21+0×20=4+2+0=6
Và dãy nhị phân 10001 biểu diễn trong hệ thập phân là
1×24+0×23+0×22+0×21+1×20=16+0+0+0+1=171×24+0×23+0×22+0×21+1×20=16+0+0+0+1=17
Bạn có thể hiểu rằng dãy nhị phân chỉ chứa duy nhất hai giá trị là 0 hoặc 1, khi bạn viết một số dưới dạng tổng liên tiếp các lũy thừa của 2, các hệ số khác là không cần thiết.
III. CỘNG THEO CÁCH CHƠI NIM
Bí mật để tìm ra chiến lược thắng nằm ở cách viết số kích thước của các đống (số lượng đồng xu của từng đống) theo dạng nhị phân và cộng chúng lại với nhau, nhưng không phải cộng theo cách thông thường, mà là cộng theo một cách khác, gọi là “Phép cộng Nim”.
Để cộng một số số nhị phân cho trước bằng “phép cộng Nim”, đầu tiên bạn viết chúng theo dạng cột (viết số sau đứng dưới số trước), như cách thực hiện phép cộng thông thường. Sau đó bạn nhìn từng cột theo thứ tự. Nếu số lượng các con số 1 là lẻ, bạn viết 1 ở dưới chúng, nếu số lượng chẵn, viết số 0 dưới chúng. Làm như vậy với từng cột cho ra số nhị phân mới, và đó là kết quả của “phép cộng Nim”.

Một trong những trò chơi máy tính đầu tiên có tên là Nimrod, được thế kế để chơi trò chơi Nim.
Trò chơi này được triển lãm vào năm 1951 tại Festival Anh quốc
Ví dụ, hãy cộng (theo cách Nim) các số nhị phân 10, 11, và 100 (các số này biểu diễn dưới thập phân là 2, 3 và 4):
![]()
Vậy kết quả của “phép cộng Nim” là số số nhị phân 101. “Phép cộng Nim” không giống với phép cộng thông thường, số nhị phân 101 là 5 ở hệ thập phân, không bằng với phép cộng thông thường là 2+3+4=92+3+4=9
IV. AI THẮNG CUỘC?
Khi Charles Bouton phân tích trò chơi Nim, ông phát hiện ra 2 điều nắm giữ chìa khóa dẫn đến chiến lược thắng.
Điều 1: Giả sử đến lượt bạn và tổng Nim các đồng xu trong các đống bằng 0. Cho dù bạn làm gì đi nữa, tổng Nim các đồng xu sau khi bạn thực hiện nước đi đều khác 0.
Điều 2: Giả sử đến lượt bạn và tổng Nim các đồng xu trong các đống khác 0. Lúc đó, luôn có một nước đi đảm bảo rằng sau khi bạn thực hiện nước đi, tổng Nim các đồng xu trong các đống bằng 0.
Không khó để chứng minh các điều trên luôn đúng, nhưng bạn có thể tự trải nghiệm bằng cách chơi với các đống xu.
Bây giờ giả sử bạn là người chơi A, bạn đi trước, cũng giả sử rằng tổng Nim số lượng các đồng xu trong các đống khác 0. Chiến lược của bạn như sau: Đi nước đi sao cho có thể làm giảm tổng Nim tiếp theo (tổng Nim sau khi bạn đi) về 0. Điều này nghĩa là cho dù B đi thế nào ở nước kế tiếp thì theo “điều 1” nước đi đó sẽ biến tổng Nim tiếp theo thành một số khác 0.
Chúng ta hãy xem tổng Nim trong bảng sau:

Các giá trị 0 và khác 0 của tổng Nim theo bảng trên sẽ đảm bảo bạn là người chiến thắng! Nếu B thắng, B sẽ thực hiện nước đi không chừa lại đồng xu nào, nghĩa là B sẽ tạo ra nước đi mà kết quả tổng Nim bằng 0 mà như chúng ta đã thấy là không thể. Ngược lại, nước đi của bạn luôn làm tổng Nim giảm về 0 và tại một số thời điểm của trò chơi thì tổng Nim bằng 0 sẽ tương ứng với không còn đồng xu còn lại, khi đó bạn thắng.
Điều này chỉ ra rằng nếu tổng Nim các đồng xu trong các đống ở thời điểm bắt đầu khác 0, thì A có chiến lược thắng. Chiến lược này luôn tạo ra nước đi làm giảm tổng Nim tiếp theo về 0. (Bạn có thể kiểm tra điều này bằng cách xem đây là chiến lược được A chơi trong ví dụ ở đầu bài viết.)
Nếu tổng Nim các đồng xu trong các đống ở thời điểm bắt đầu của trò chơi bằng 0, thì B là người có chiến thuật thắng. Cho dù A có đi nước đầu như thế nào thì kết quả tổng Nim vẫn khác 0 khi đến lượt B và như đã đề cập ở trên, điều này có nghĩa B có chiến lược thắng.
V. PHÉP CỘNG NIM THỐNG TRỊ THẾ GIỚI
Phép cộng Nim rõ ràng rất có lợi khi chơi trò chơi Nim, nhưng phép cộng Nim chỉ có tác dụng trong trò chơi này, đúng chứ? Sai rồi! Thật ra trong mỗi ngày ta đều sử dụng cách cộng số kỳ lạ này.
Máy tính là thiết bị nhị phân. Tất cả thông tin lưu trữ (bao gồm các con số) được chuyển hóa thành các dãy 0 và 1. Nhưng máy tính không chỉ lưu trữ dữ liệu, chúng còn thực hiện được các lệnh logic, dựa trên câu trả lời có/không. Ví dụ, cho một tên tài khoản và mật khẩu, máy tính tự hỏi:”Đây có là tài khoản chính xác?” và “Đây có là mật khẩu chính xác?” và dựa trên câu trả lời để quyết định có để người dùng truy cập vào hay không. Lưu ý rằng các lệnh này dùng 2 lệnh nhập (tài khoản đúng? Mật khẩu đúng?) và xuất ra một lệnh (truy cập hoặc không truy cập),
Viết 0 cho giá trị “không” và 1 cho giá trị “có”, những lệnh logic này cũng có thể chuyển hóa thành dãy nhị phân chứa các số 0 và 1. May mắn thay, hóa ra tất cả các lệnh logic bạn muốn thực hiện được tạo ra từ 6 loại cơ bản. Bạn đơn giản chỉ cần thiết lập đúng cách.

Máy tính là thiết bị nhị phân
Một trong những lệnh cơ bản là XOR. Lệnh này cần 2 đầu vào (input), mỗi đầu vào có giá trị 0 hoặc 1, và chuyển thành một đầu ra (output), cũng có giá trị là 0 hoặc 1. Đây là bảng chân trị XOR
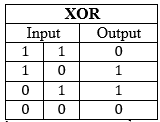
Nhìn kĩ hơn thì ta thấy rằng XOR giống hoàn toàn với tổng Nim của các số 0 và 1:
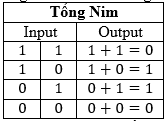
Do đó, rất nhiều lệnh mà máy tính của bạn thực hiện hằng ngày đều dựa trên tổng Nim. Không có máy tính, mọi thứ sẽ rất khác.
Bài viết do thành viên Chuyên san EXP dịch.