Những người đàn ông và phụ nữ hài lòng bao nhiêu với phép nối x được tạo bởi thuật toán Gale – Shapley? Ví dụ, có thể tìm thấy một phép nối ổn định y khi một số người đàn ông thích người tình y hơn x? Có một phép nối ổn định y ở một số người phụ nữ thích người tình y hơn là ở x?

 

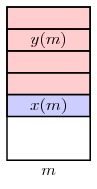
Chúng ta sẽ nhìn thấy rằng không có người đàn ông nào thích người tình của họ ở trong một phép nối ổn định khác người tình trong x. Điều đó có nghĩa là nếu y là một phép nối ổn định khác, thì hoặc là y(m)=x(m) hoặc m thích x(m) hơn y(m). Do đó chúng tôi gọi x là một phép nối ổn định tối ưu của M. Tại một thời điểm nào đó sẽ thuyết phục bạn rằng chỉ có một phép nối ổn định tối ưu của M

 

Hãy giả sử tồn tại phép nối y khác và người đàn ông m sao cho m thích y(m) hơn x(m). Ta sẽ thấy rằng điều này là không thể nếu y là phép nối ổn định.

 

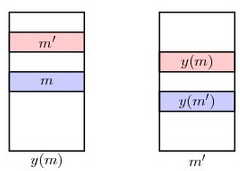
Trong trường hợp này, chúng tôi sẽ cho rằng các bước của thuật toán Gale dần đến phép nối ổn định x. Vì m thích y(m) hơn x(m) nên y(m) phải từ chối m tại một bước k của thuật toán. Tất cả m kiểu này, chọn một m sao cho không có người đàn ông m′′ nào bị y(m) từ chối sớm hơn một bước k′<k

Khi y(m) từ chối m, cô ấy phải thích một người đàn ông m′ đã cầu hôn cô ấy ở bước k. Khi m′ được y(m)) chấp nhận ở bước k và chưa bị y(m′) từ chối ở bước trước k, m′ phải thích y(m) hơn y(m′).

Vì thế y(m) thích m hơn m và m′′ thích y(m) hơn y(m′) nghĩa là y không phải là sự kết hợp ổn định.

Bằng cách này, chúng ta thấy rằng x là một phép nối ổn định tối ưu của M, mọi người đàn ông ít nhất hài lòng với người tình x cũng như phép nối ổn định y

 

Ví dụ đơn giản cho thấy phép nối x không phải luôn tối ưu cho phụ nữ. Tuy nhiên, có một phép nối ổn định tối ưu W, chúng ta chỉ cần áp dụng thuật toán Gale – Shapley với vai trò thay đổi cho nhau, tức để phụ nữ cầu hôn nam giới.

 

Tiết lộ sở thích thực sự

 

Ta có thể tạo ra phép nối ổn định với thuật toán Gale-Shapley và những phép nối này là tốt nhất có thể cho một tập người. Cho đến nay, chúng ta đã giả định rằng mỗi người thể hiện trung thực sở thích thật sự của mình. Tuy nhiên, có khả năng một người đàn ông có thể cố lấy một người tình hấp dẫn hơn bằng cách miêu tả sai sở thích thật sự của mình.

 

Chúng tôi sẽ cho thấy rằng tiết lộ sở thích thật sự của một người, theo lý thuyết trò chơi, là một chiến lược trội cho nam giới. Điều này có nghĩa rằng, giả sử tất cả những người đàn ông và phụ nữ khác giữ sở thích như nhau, một người đàn ông không thể có được một người tình hấp dẫn hơn bằng cách miêu tả sai sở thích của mình.

 

Đặt P là tập hợp các sở thích của tất cả những người đàn ông và phụ nữ, ta giả định đó là sở thích thật sự của họ. Ta muốn xem xét tập các sở thích P′, giống P ngoại trừ một người đàn ông mm, người mà ta gọi là “kẻ gian dối.”

 

Ngoài ra, ta sẽ sử dụng x = GS (P) để biểu thị các phép nối ổn định là kết quả của thuật toán Gale – Shapley áp dụng với các sở thích thật sự P, trong khi y= GS (P ′) là phép nối ổn định từ các sở thích gian dối. Mục tiêu của ta là để cho m không thể lợi dụng bạn tình của mình; nói cách khác, ta sẽ cho thấy rằng hoặc là y (m) = x (m) hoặc m thích x(m) hơn y(m) dựa theo sở thích thật sự của mình.

 

Đầu tiên, ta thấy rằng ta chỉ cần phải xem xét một trường hợp cụ thể của việc miêu tả sai. Luôn nhớ rằng y = GS (P), chúng ta sẽ xem xét tương đương miêu tả sai đơn giản P′″ có những tính chất mà kẻ gian dối mm thích y(mm) hơn tất cả người phụ nữ khác, theo danh sách sở thích của ông trong P″. Đó là, kẻ gian dối mm lấy P′″ từ P bằng cách di chuyển người tình của mình trong y để lên đầu danh sách. Ta ký hiệu z = GS (P″) là phép nối ổn định có kết quả từ việc miêu tả sai đơn giản P′′.

 

Ta quan sát các điều sau:

 

1.y(mm) = z (mm).Điều này có nghĩa rằng miêu tả sai P′′″ dẫn đến cùng một người tình cho mmnhư miêu tả sai P′′. Đây là lý do tại sao ta nói rằng P′ và P″ là miêu tả sai tương đương. Nếu mm không có được một người tình hấp dẫn trong z, anh ta sẽ không có y và ngược lại.

 

Điều này rất dễ hiểu. Hãy nhớ rằng y là ổn định đối với các sở thích của P′ vì ta sử dụng thuật toán Gale – Shapley để thu được y. Điều này có nghĩa rằng không có người đàn ông m cũng như người phụ nữ w thích nhau (trong P′) hơn người tình của họ trong y. Tuy nhiên, điều này hàm ý rằng y là ổn định trong P′′, người duy nhất có sở thích đã thay đổi là mm , từ khi ông ta di chuyển y(mm) lên đầu danh sách của mình trong P″, ông tìm thấy người tình của mình dưới y theo P′′ ″ với mức độ mong muốn như trong P′.

 

Cần nhớ rằng bây giờ z  là phép nối ổn định tối ưu M theo P′″. Vì y ổn định đối với P′″ nên mm thích z(mm) ít nhất là như tình cảm của anh ta đối với y(mm). Tuy nhiên, ông vẫn thích y(mm) (trong P″) hơn bất kỳ người phụ nữ khác, vì vậy z(mm) = y(mm)).

 

2. Bây giờ chúng ta sẽ cho rằng P′′.  đại diện đơn giản cho kẻ gian dối mm và y = GS(P′). Ta cũng giả định rằng mm trình bày sai sở thích thật sự của mình để có được người tình y(mm) mà anh thích ít nhất cũng như x(mm), dựa theo sở thích thật sự P của anh ta. Với những giả thiết này, không có người đàn ông nào trong y tồi tệ hơn anh ta trong x, dựa theo sở thích thật sự của anh ta. Điều này có nghĩa đối với mỗi người đàn ông m, hoặc là y(m) = x(m) hoặc m thích y(m) hơn x(m).

 

Chú ý, chúng ta giả sử rằng mức độ chi phí gian dối không quá tệ đối với y. Trên thực tế, ông ta đã trình bày sai nhằm hi vọng người tình trong mộng đồng ý yêu ông.

 

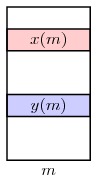
Bây giờ giả sử có một người đàn ông m có chi phí tệ trong y hơn trong x, tức là giả sử m thích x(m) hơn y(m) như hình vẽ. Vì m không phải là kẻ gian dối, m thích cả P và P′. Do đó m đã bị x(m) từ chối tại một số bước trong GS(P′).

Đặt k là bước đầu tiên, trong đó một số người đàn ông m bị x(m) từ chối trong GS(P′). Cụ thể hơn, giả sử m bị x(m) từ chối và tạo ưu thế cho m′ ở bước k, điều này có nghĩa là x(m) thích m′′ hơn m, do đó không thể có chuyện m cầu hôn x(m) trong GS(P). Do đó m′ thích x(m′) hơn x(m).

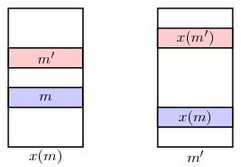
Vì m′′ cầu hôn x(m) ở bước k trong GS(P′) nên m phải nhận được lời từ chối từ x(m′) ở một bước trước đó trong GS(P′). Tuy nhiên, điều này là không thể vì ta giả sử k là bước đầu tiên mà m bị x(m) từ chối trong GS(P′)Do đó m thích y(m) ít nhất cũng như thích x(m)

 

3. Vì mọi người đàn ông m đều hài lòng với y(m)cũng như x(m), ta rút ra kết luận rằng: Nếu m cầu hôn một người phụ nữ w trong GS(P′) thì anh ta phải cầu hôn cô trong GS(P)

 

Từ quan sát này ta rút ra một thực tế rất hữu dụng rằng nếu w  chỉ nhận được một lời đề nghị trong GS(P) cô ta cũng chỉ nhận được một đề nghị trong GS(P′). Nếu đề xuất này là của m, thì x(m)=y(m)=w

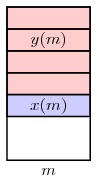
Bây giờ ta sắp xếp tất cả mọi thứ ta cần nhằm giải thích lí do vì sao nói ra sở thích thật sự là chiến lược trội cho nam giới. ta giả sử rằng các người đàn ông và phụ nữ còn lại đều có sở thích như nhau, và chúng ta sẽ thấy kẻ gian dối không thể thu hút người tình mà anh ta thích, khi đó hoặc y(mm)=x(mm) hoặc m thích x(mm) hơn y(mm)

 

Chúng ta sẽ bắt đầu bằng giả thiết rằng đối với kẻ gian dối, hoặc là y(mm)=x(mm) hoặc m thích y(m) hơn x(mm) vì kết quả này chắc chắn đúng nếu như mm thích x(mm) hơn y(mm)

 

Với giả thiết này, chúng ta thấy rằng, trong y không có người đàn ông nào tệ hơn x, như đã giải thích ở trên. Ngoài ra nếu như m cầu hôn một phụ nữ w, người chỉ nhận được một lời cầu hôn, khi đó y(m)=x(m)

 

Nhìn vào các bước của GS(P), kẻ gian dối sẽ cầu hôn với người phụ nữ x(mm) anh ta muốn làm người tình ở bước r nào đó. Chiến lược của tôi sẽ cho thấy rằng, mọi người đàn ông m cầu hôn x(m) ở bước r hay trễ hơn sẽ có y(m)= x(m) Khi đó suy ra được rằng: y(mm)= x(mm)

 

Chúng ta tiến hành bằng cách, đầu tiên nhìn vào người đàn ông m, người đàn ông này cầu hôn x(m)=w trong bước cuối cùng t của GS(P)

Khi đó m là người duy nhất cầu hôn w. Nếu không, w phải từ chối người đàn ông trước kia cô đã chấp nhận, và người đàn ông đó sẽ thực hiện lời cầu hôn khác trong bước tiếp theo. Do vậy y(m)=x(m)

 

Bây giờ, chúng ta xét đến người đàn ông đã cầu hôn x(m)=wlà người phụ nữ phù hợp với mình ở bước r≤s<t, và ta sử dụng giả thiết quy nạp rằng bất kì người đàn ông nào tỏ tình với người tình của mình ở bước s+1+1 thì thỏa mãn y(m)=x(m)

Sau đó chúng ta nhìn vào tập các người đàn ông ¯M¯ mà bị w từ chối trước khi chấp nhận lời cầu hôn của m. Nếu không có ai bị w từ chối, khi đó m là người đàn ông duy nhất cầu hôn w, do đó y(m)=x(m).

 

Nếu có một người nào đó bị w từ chối, kí hiệu m′ là người đàn ông cô thích nhất trong nhóm người đã cầu hôn với cô. Người đàn ông m′ này đã bị cô từ chối ở bước s đề chấp nhận m. Vì vậy m′′ cầu hôn với người tình khác ở một bước sau s, theo giả thiết quy nạp thì y(m′)=x(m′)

Vì m′′ cầu hôn với người tình tại một bước sau đó, m′ không phải là kẻ dối trá, do vậy m′′có sở thích giống nhau ở cả P và P′. Điều này có nghĩa là, khi m′ cầu hôn w  trong GS(P′)và bị từ chối, nên w có nhận được một lời cầu hôn khác trong GS(P′)

 

Ta thấy rằng nếu m cầu hôn với người phụ nữ trong GS(P′)thì anh ta cũng làm điều tương tự trong GS(P). Vì lời cầu hôn khác duy nhất mà w nhận được trong GS(P) là từ m, khi đó lời cầu hôn cuối cùng mà cô ấy nhận được trong GS(P′)cũng từ m. Vì vậy, ta kết luận rằng y(m)=x(m)

 

Do đó bất kì người đàn ông nào ngỏ lời với người tình của mình ở bước s thì y(m)=x(m). Theo quy nạp cho thấy rằng, nếu người đàn ông nào đó cầu hôn với người tình của mình ở bước r hoặc sau bước r thì phải thỏa mãn y(m)=x(m). Vì kẻ dối trá cầu hôn với người tình ở bước r, , điều này có nghĩa là y(mm)=x(mm) Nói cách khác, kẻ dối trá không thể cải thiện độ ấn tượng của người tình về mình khi hắn không thật lòng.

Lạ thật, ví dụ cho thấy rằng, những người đàn ông khác cầu hôn với người tình của họ trước bước r có thể cải thiện độ ấn tượng của người tình về họ. Tính cách không thật lòng của kẻ dối trá mm  không thể cải thiện độ ấn tượng của người tình về mình mà còn giúp cải thiện ấn tượng của cô ta cho người đàn ông khác.

 

Tổng kết

Trở lại câu hỏi về phép nối giữa học sinh với trường học. Chúng ta nên hỏi nhóm sẽ đưa ra nguyện vọng (hay lời cầu hôn trong ví dụ trên). Chạy thuật toán với trường hợp học sinh đưa ra nguyện vọng khiến cho các học sinh không có động lực để đưa ra nguyện vọng trái với ý muốn bản thân mặc dù trường học khuyến khích như vậy. Tuy nhiên, chúng ta mong đợi rằng việc nhà trường đưa ra chỉ tiệu không đúng với chỉ tiêu thật sự sẽ được áp dụng chung cho các học sinh, khi đó học sinh sẽ dễ dàng xác định. Trường học có thể bị khống chế phải thông qua các yêu cầu rõ ràng hoặc các điều luật khác nhằm ngăn chặn đưa ra chỉ tiêu không đúng, ví dụ như phân biệt chủng tộc.

 

Trên thực tế, một trong những cộng tác viên của Roth là Atila Abdulkadiroglu nói rằng ông đã nhận được các cuộc gọi từ các bậc cha mẹ muốn nghe lời khuyên của ông nhằm chuẩn bị tốt hơn cho việc chọn trường của con họ. Câu trả lời của ông rất đơn giản:” Sắp xếp các trường theo đúng thứ tự ưu tiên”.

 

Tính ổn định là một điều kiện trực quan cần thiết khi áp dụng trên hệ phép nối, như quy trình tuyển sinh ở trường Thành phố New York. Trong một phép nối ổn định, không có một tổ chức nào khuyến khích tìm kiếm các phép nối khác nhau; Ví dụ như: Nếu một người đàn ông có tình cảm với một người phụ nữ hơn vợ của anh ta, thì anh ta không có cơ hội đâu vì cô ấy còn có tình cảm với chồng mình hơn anh ta.

 

Tuy nhiên, người ta có thể hỏi có chứng cứ nào ủng hộ tính quan trọng của vai trò ổn định trong hệ phép nối. Trên thực tế, Roth và công sự của ông đã nghiên cứu trên nhiều thị trường khác nhau để giải đáp cho câu hỏi này. Ví dụ, quy trình các sinh viên y khoa Mỹ được nối với các chương trình cư trú đã được sửa đổi trong những năm 1950 và trở nên gần giống với thuật toán chấp nhận trì hoãn. Và thuật toán này đã được chứng minh rất thành công, kết quả là Ủy ban Hoàng gia Anh (British Royal Commission) đã đề nghị từng phân khu của Dịch vụ Y tế  Quốc gia Anh (British National Health Service) đưa vào sử dụng một hệ tương tự.

 

Đúng như mong đợi, mỗi phân khu đã sử dụng thuật toán phép nối khác nhau một chút vì các chi tiết trong hệ ở Mỹ không được miêu tả trong các tài liệu y khoa nước Mỹ. Hệ này ở một số phân khu được phát triển tốt trong khi một số khu khác lại thất bại. Roth và các cộng sự của ông xác định rằng thuật toán chỉ thành công khi có tính ổn định, còn không có tính ổn định thì thất bại.

 

Về việc áp dụng lý thuyết trò chơi vào kinh tế, Roth đã viết: “Kiểm tra thực tế thành công của chúng tôi không chỉ đơn thuần là việc chúng tôi hiểu rõ những nguyên tắc chung để điều khiển tương tác kinh tế tốt như thế nào, mà còn cho thấy rằng ta có thể áp dụng những kiến thức này rất tốt vào các câu hỏi thiết thực trong kĩ thuật kinh tế vi mô”. Thật vậy, các ví dụ như quy trình tuyển sinh vào trường trung học Thành phố New York là một bằng chứng quan trọng thể hiện sự thành công của thuật toán này.